前回の記事では、Pythonを利用して、作成した正弦波の音声をFFT処理し、周波数のグラフ化までを行いました。
今回の記事では、周波数データに変換したピー音の周波数を変更し、元の波形に戻すとどうなるか実験してみます。
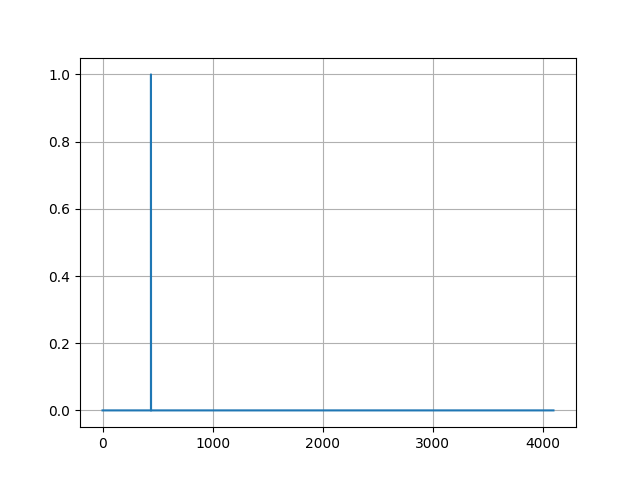
その前に、前回の記事で出力したFFTのデータをもう一度良く見て見るために、少しプログラムを変えてグラフ出力します。具体的には20行目に下記変更を加えて、データ全体をグラフに表します。
【変更前】plt.plot(freq[1:int(N/2)], Amp[1:int(N/2)])
【変更後】plt.plot(F.imag[1:N])
実行して得られた周波数領域のグラフが以下になります。
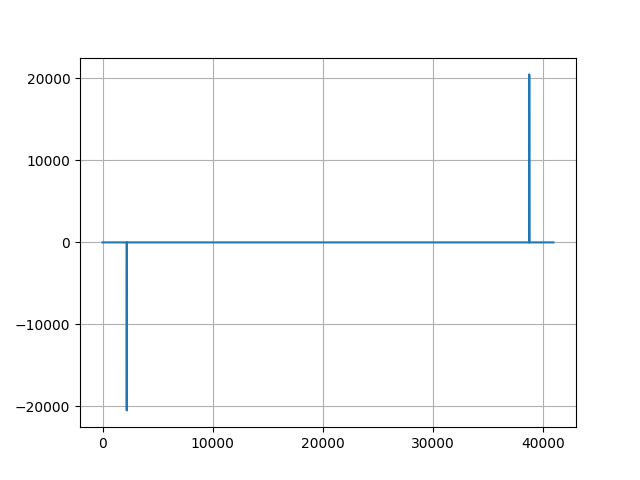
続いて、7行目に下記変更を加えて周波数を変更します。
【変更前】f0 = 440
【変更後】f0 = 880
実行して得られた周波数領域のグラフは以下になります。
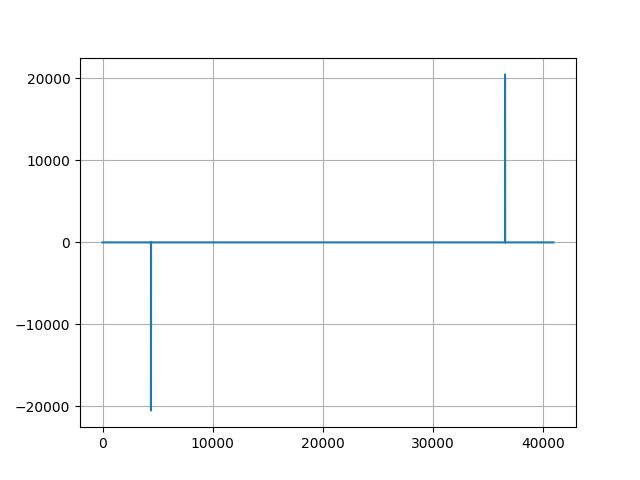
図1 440Hzの周波数グラフと図2 880Hzの周波数グラフの違いを確認してみましょう。
図2のほうが縦棒が中央に寄っていることがわかると思います。
これは周波数が上がれば、周波数領域のデータが中央に寄ることを意味しています。
この結果を元に、440Hzの音声データをFFTし、周波数データを中央に寄せて、逆FFTで元の音声データに戻してみます。
プログラム全体は下記となります。
少し長くなりましたので、周波数変更処理の部分は関数として定義(7行目から46行目)しています。
48行目から86行目がメイン処理になります。
メイン処理はやっていることは単純なので、流れのみ説明します。
1.440Hzの正弦波を作成し、グラフ化しています。
2.440HzのデータをFFTし、周波数データに変換しています。
3.周波数データを新たに定義したshift_freqという関数を使って440Hzプラスします。
4.変更した周波数データに対して、逆FFT処理をかけて元の波形に戻し、グラフ化します。
5.元に戻したデータをWaveファイルとして出力しています。
続いて、shift_freqの処理について解説していきます。
7行目で、「shift_freq」という関数を定義しています。引数として、FFTの実行結果、シフトする周波数、サンプリング周波数、音声の長さ(秒)を定義しています。シフトする周波数はプラスでもマイナスでも構いません。今回のメイン処理ではわかりやすいように440Hzプラスし、880Hzにしています。
8行目で、サンプリング周波数に音声の長さ(秒)を乗算して、信号データの総数Nを算出しています。
9行目では、シフトする周波数に音声の長さ(秒)を乗算して、実際にシフトする量を算出しています。
10行目から27行目で、周波数をプラス方向にシフトする場合の処理を定義しています。
13行目から19行目のループでは、データの中央部から左方向に向かって値を見ていき、シフト分先(si)にある値を現在(i)の位置にシフトします。シフト分先(si)がマイナスになったら、現在(i)の位置に0を入れます。
21行目から27行目のループでは、データの中央部から右方向に向かって値を見ていき、シフト分先(si)にある値を現在(i)の位置にシフトします。こちらもシフト分先(si)が総数Nを超えたら、現在(i)の位置に0を入れます。
28行目から45行目の処理は、周波数をマイナス方向にシフトする場合の処理を定義しています。
処理内容の説明はプラス方向と同様のため割愛します。
最後の46行目でシフトしたFを戻り値としてメイン処理に渡して関数処理は完了します。
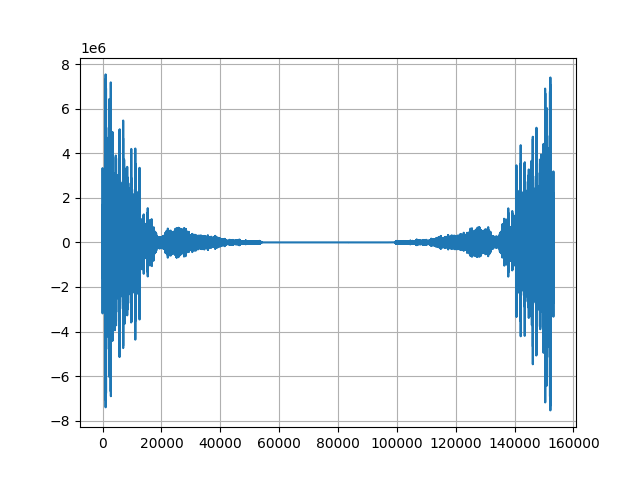
本プログラムを実行して得られた波形画像は以下になります。
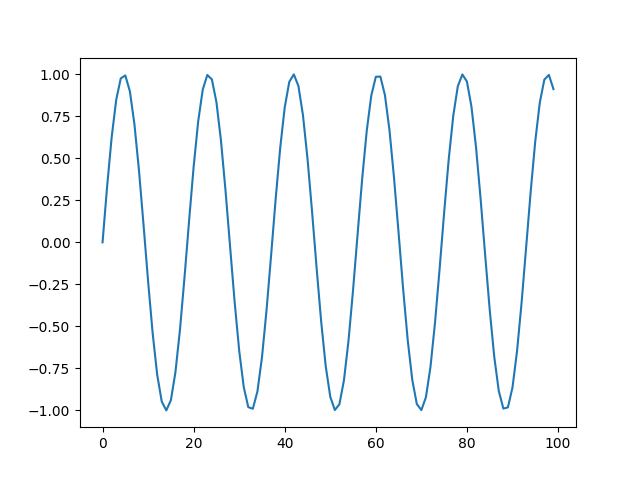
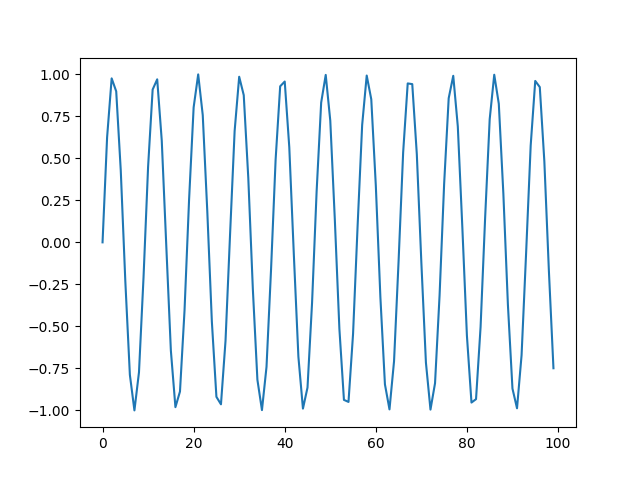
図3が作成した440Hzの波形で、図4が、440Hzの波形をFFTして440Hzシフトし880Hzとして、波形データに戻したものです。周波数を上げたので波形が細かくなっているのがわかります。
音声でも確認してみましょう。音量にご注意ください。
プー音からピー音になりましたね。
周波数領域のデータをシフトすることで、周波数を変更できることが確認できました。
次の記事では、作成した波形ではなく、実際の音声を利用して処理してみたいと思います。
コメント