前回の記事で、ピー音を作成し、グラフ化、Waveファイル化の処理まで作成しました。
今回は、Pythonによる音声処理の続きで、周波数をグラフ化するところまで実装します。
周波数のグラフを算出するには、FFTという処理を実行します。
FFT:高速フーリエ変換は、離散フーリエ変換と呼ばれる周波数解析手法を高速化したアルゴリズムです。内部的にとても複雑な処理を行っていますが、Numpyのライブラリとして利用することが可能で、Pythonのプログラムとしては数行で利用可能です。
それではプログラムを見ていきましょう。
1行目から14行目については、前回の記事で紹介したプログラムと同一です。
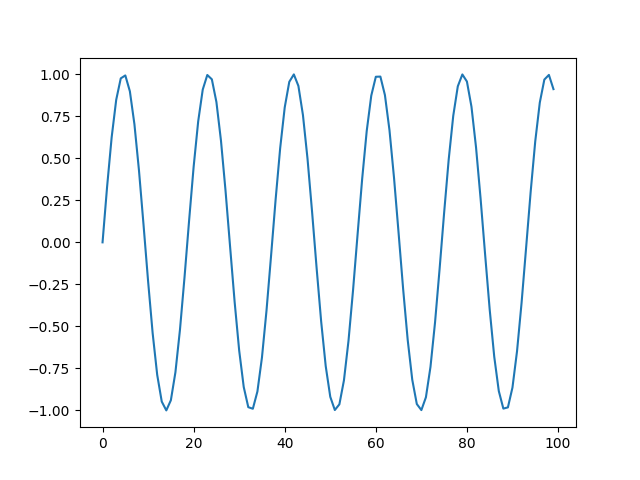
440Hz(音階のラ)のピー音の波形データを算出しています。
今回追加したプログラムは16行目から23行目です。
17行目で、作成したピー音の波形をNumpyのFFTを利用して周波数データに変換しています。
18行目では、グラフのX軸に適用する周波数軸を算出しています。
19行目では、グラフのY軸に適用するデータの振幅を調整しています。
20行目〜23行目で、グラフ化を行い、sin_freq.pngというファイルとして出力しています。
出力されたファイルは以下です。
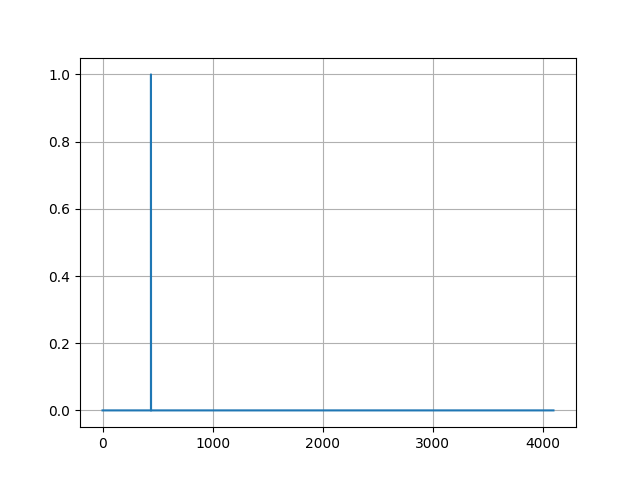
分かりづらいですが、440Hzのところでグラフが1になっていることが確認できます。
簡単ですが、今回はここまでです。
次の記事では、FFTで得られた周波数領域のデータを変更して、元の波形に戻してみます。
コメント