前回の記事では、ピー音を作成し、FFT処理後、周波数を変更して、逆FFTにより音の高さが変わるところまで確認しました。
今回は、いよいよ実際の音声の処理を実行してみようと思います。
今回用意したプログラムは以下のとおりです。
細かい処理内容の説明は割愛しますが、プログラムの流れとしては下記となります。
1.音声ファイルを読み込む
2.音声ファイルの情報を読み込む
3.音声ファイルをFFT処理し、周波数をグラフ表示する
読み込んでいる音声ファイルは以下です。Webのフリー素材で拾ってきたものになります。
音量にご注意ください。
このプログラムを実行して、得られた周波数グラフは以下になります。
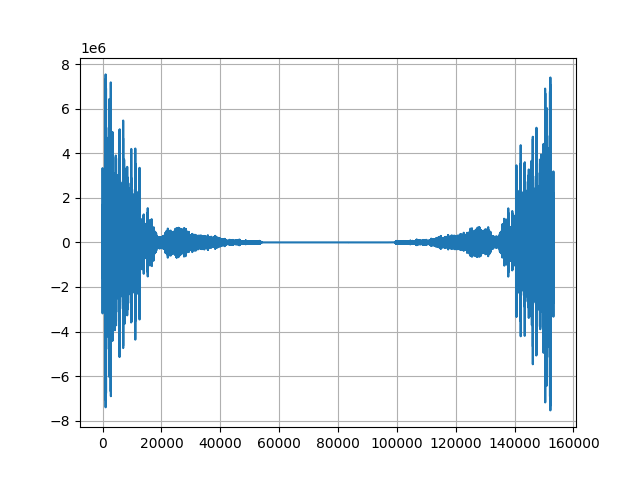
前回の記事でピー音の周波数を確認したときと比べて、随分複雑になっていることがわかります。
これは実際の音声には複数の音波が混ざり合っていて、周波数が複数あることを意味しています。
実はリアル音声を周波数解析する上で、課題が大きく2つあります。
課題1 時間とともに音波および周波数が変化すること
課題2 周波数が複数混合しているため、周波数シフトの方法を工夫しなければならないこと
それぞれの課題について、解説していきます。
課題1 時間とともに音波および周波数が変化すること
通常の音声はピー音と違い、時間とともに変化します。
今回のプログラムで確認した音声は、3秒程度ですが、通常の音声はより長くなります。
より長いデータをそのままFFTすると音声全体の周波数をざっくりとしか解析できません。
ざっくりとした周波数をシフトした場合、逆FFTで戻した際の音質が落ちてしまいます。
こういった課題を解決するために、音声処理の世界では、音声を一定の時間で切り刻んで解析するのが一般的です。
ただし、単純に切り刻むだけだと逆FFTで戻した音声の繋がりが悪くなるため、オーバーラップ処理と窓関数処理を実施します。
オーバーラップ処理は、音声を単純に切り刻むのではなく、前後を重ねて切り刻む処理です。
イメージは以下のような感じです。①〜⑦の前後が重なったデータを処理対象とします。
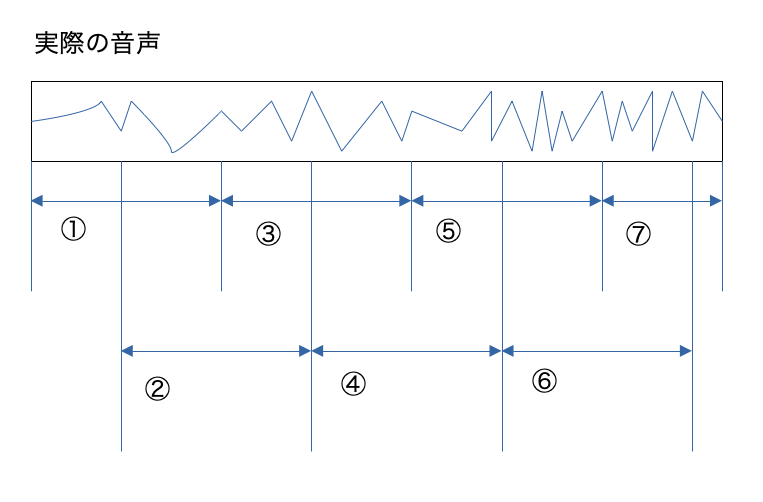
窓関数は、信号の最初と最後がゼロになるように丸める処理です。実信号に掛け合わせて利用します。窓関数により、オーバーラップされた部分の繋がりが良くなります。
課題2 周波数が複数混合しているため、周波数シフトの方法を工夫しなければならないこと
ピー音では440Hzの音程のみの信号でしたが、実際の音声には複数の周波数が含まれます。
前回の記事でシフト処理を行った際、440Hzを加算して880Hzとしましたが、複数の周波数が含まれる場合は、加算によるシフトで不都合が生じます。
下記は音階に対応する周波数を表しています。
| 音階 | 周波数(Hz) | 一つ前の音階との差分 | 一つ前の音階との倍率 |
|---|---|---|---|
| ド | 261.626 | − | − |
| ド# | 277.183 | 15.557 | 1.0595 |
| レ | 293.665 | 16.482 | 1.0595 |
| レ# | 311.127 | 17.462 | 1.0595 |
| ミ | 329.628 | 18.501 | 1.0595 |
| ファ | 349.228 | 19.600 | 1.0595 |
| ファ# | 369.994 | 20.766 | 1.0595 |
| ソ | 391.995 | 22.001 | 1.0595 |
| ソ# | 415.305 | 23.310 | 1.0595 |
| ラ | 440.000 | 24.695 | 1.0595 |
| ラ# | 466.164 | 26.164 | 1.0595 |
| シ | 493.883 | 27.719 | 1.0595 |
| ド | 523.251 | 29.368 | 1.0595 |
一つ前の音階との差分は、音程が上がるにつれて増えていっているのがわかります。
一方、一つ前の音階との倍率は、一定となります。
つまり、周波数を変更する場合、加算ではなく、乗算する必要があるということです。
リアル音声処理では、これらの課題を解決していく必要があります。
次回の記事では、実際の音声処理で必要となる、オーバーラップ処理と窓関数処理を実装していきます。
コメント